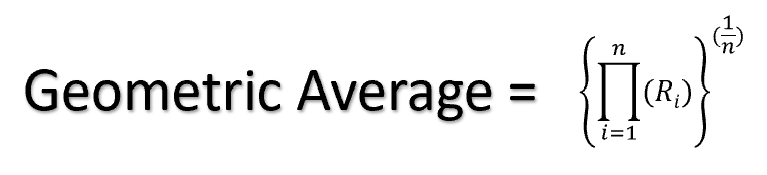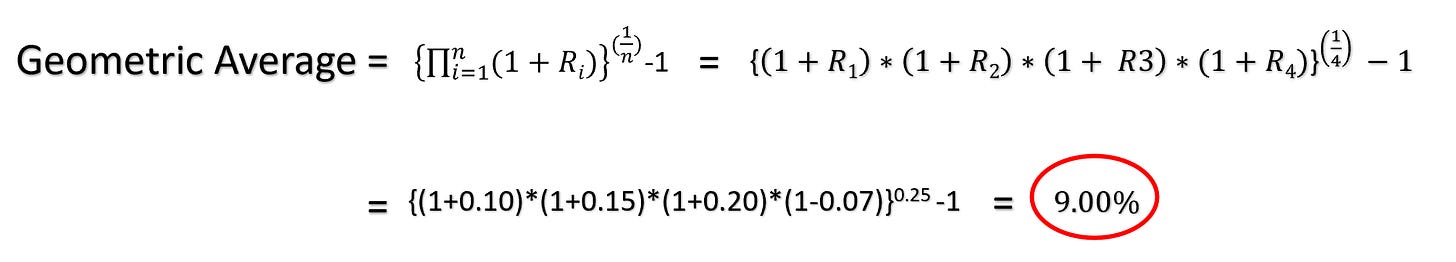On Averages - Your Average Return is Geometrically Different Than What 'Average Return' Means
aka. Don’t Use The Wrong Mean Or You’ll be Off Central…While Drinking Your Juice In The Hood
The title is a mouthful, but I wanted to go hard with the puns…Also, “Don’t Be A Meance To South Central While Drinking Your Juice In The Hood”, is a fond memory of my childhood and as I typed a sentence with “mean”, “off-central”, and “don’t” I couldn’t not include it as my image theme.
Don’t let the movie references distract you, however, because the topic of ‘what does average mean’, is hugely important to your actual retirement planning.
What if the “Average” return for the S&P500 was 10%, but actually investing in the S&P500 would only grow your portfolio at an average rate of 9%? How is it possible? How is your average return 10%, but your portfolio only grew 9% a year?
If you recall from previous posts, a little difference in return can lead to huge differences in your portfolio when compounding over a long investment horizon. A 1% different ‘average’ return can lead to $100s of thousands of dollar difference in your ending portfolio.

So is it possible to have 2, or more, different ‘average’ returns and have all the numbers be calculated correctly?
And even more important for you, how does this difference impact your investment portfolio?
What is Average?
How do you define average?
One definition may be: Average is significantly “larger than your [insert joke here… IQ? Physique? weenis?]”
But more likely you thought of words like “expected”, “the middle”, “center”, or “representative”. Possibly you Goldilocks-ed it and thought “not too high, not too low, just medium”.
Maybe if you are mathematically inclined you thought of summing up a bunch of numbers and dividing by the count to get a representative single number of the entire set.
For the amount ‘average’ is used, you would think ‘average’ was a very well-defined measure. Archimedes or Pythagoras or even Diophantus, who was like an Algebra O.G., would have written some paper about average.
But ‘Average’ is actually not a mathematical term.
It is why you had to learn mean, median, and mode in school and the technical name is ‘central tendency’ not average. Central tendencies are exactly that, where the center or middle of a set tends to be.
Don’t worry, we aren’t going to talk about median and mode here other than a quick example - we are going to focus on the mean aka what you think of when someone says average.
[Note - for simplicity, I’ll refer to the mean as average for most of the post just because it will read more natural for most]
What Is The Goal Of Calculating Average
First, we need to define the goal of taking the average - or really the goal of any measure of central tendencies.
You use the central tendency metric to try to simplify a data set into 1 representative number.
That is why there is so many different measures of central tendency. Depending on the question you are trying to answer will drive which calculation you should use.
Choosing the wrong ‘average’ can lead to the wrong conclusion.
Example: If you were given the following set of numbers, what would the average be?
You have 10 numbers clustered between 4-6, with 5 occuring 6 times. If you had to pick a representive number for this set, does it make sense to use the arithmetic mean of 69? (Other than yes, it always makes sense to answer 69 (nice)).
What is a better ‘average’? Depends on the task at hand.
If you were playing a card game. There are 11 cards in a shuffled deck. You get 1 guess at which card gets flipped over. You don’t know what numbers are in the deck, all you are given is the a single representative number to use.
Do you want the mean? If someone said there are 11 cards and the average is 69, what would you guess the number on the card would be?
For this use, the best representative number (ie- the one that is most likely to help you guess the right card) would be 5 since it occurs the most. (This is the ‘mode’, the number that appears most often)
If you were measuring weenis length and only given 1 number to represent average weenis size. What is a good represenation? Probably the number right in the middle where ~50% are below the number and ~50% are above. I put the numbers in order, so you would look at the 6th number (5 below and 5 above) to get 5 units of weenis measure. Again, would you want to have everyone think the average weenis is 69 due to one massive weenis holder?
I won’t beat this point to death. But we can agree that arithmetic mean may not be the best representation of a set of numbers. (Also, you can forget about median and mode now.)
Arithmetic vs Geometric Means
There is more than 1 way to calculate the mean. For the purpose of this post we will focus on 2 ways, arithmetic & geometric means. (Note - there are others, but not relevant to our return convo).
Arithmetic means “math dealing with addition, subtraction, division, and multiplication”.
However, THE arithmetic mean is what you likely of when you think of an average. The arithmetic mean is when you sum up all the numbers in a set and divide by the count of numbers in a set.
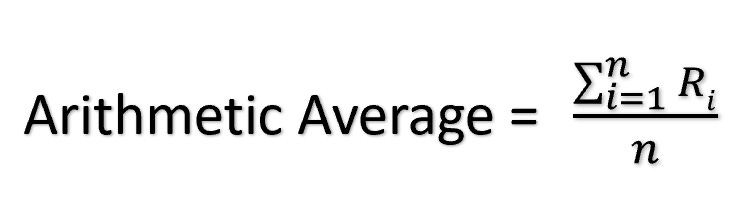
A geometric sequence is a series of numbers that each number gets multiplied by the previous numbers. (Hmm…numbers multiplied in a series…sounds almost like how stock returns are calculated period to period huh?)
The geometric average is when you take the product of a set of ‘n’ numbers and then take the 1/nth root. (Don’t worry, examples to follow).
When To Use Arithmetic Mean (Average)
Arithmetic average works well when you have numbers with a linear relationship and a fairly normal distribution without any outliers. Lots of caveats there.
In the earlier example, we saw the impact of an outlier. An outlier is a data point that is far from the rest of the points.
You don’t need one outlier, you can have a skewed distribution. Think about the annual income in the USA. You will have the vast majority of people in the $40k-$100k range. However, you have a handful of high earners who earn a lot more. There is a positive skew to the income distribution where the mean will be dragged up by the large earners.

When To Use Geometric Average
The Geometric average should be used when data shares a multiplicative relationship. It is used a lot in geometry, but outside that it is largely only used in one very important instance, calculating returns.
The geometric mean is best explained with an example. But one interesting fact to note before going to an example…The geometric average is never larger than the arithmetic average.
The geometric average only equals the arithmetic average if all the numbers in a data set are the same. IE - { 5, 5, 5, 5 } will give an arithmetic average = geometric average = 5. Otherwise, the geometric average will be a lower number.
[Note - If you have ever seen the question:
If the market goes +50%, -50%, +50%, -50%, and +50% what is the ending value. It operates at a similar principle. (Answer is you end with $84 despite 3 positve 50% vs 2 negative 50% moves)
Arithmetic average says +10% and Geometric average says -3.3%. Projecting an ‘average’ 10% is very different than an average -3.3%.
Remember a -50% move in the market needs a double (+100%) to get back to break-even. ]
Simple Example:
To make a simple example, lets say that you look at your last 4 years of investing. In no particular order, you see returns of 10%, 15%, 20%, and -7%.
Not bad, 3 good years and 1 bad year.
What is your average return?
If you take the arithmetic average you sum up 10% + 15% + 20% + (-7%) and divide by 4:
If you take the geometric average you multiple (1 + return) for each year and then take it to the 1/4th power minus 1:
Now this is where is gets to the important point.
What is the actual return you would have over the last 4 years? IE - What is the correct answer?
If you invested $100 four years ago and got a 10%, 15%, 20%, and -7% return over the 4 years, you would have:
And the correct answer is the geometric average. The geometric average will give you the average return to use to get to the same ending value.
You can check by taking the ending value of the actuals and seeing the annualized return and confirming it matches. (141.17 / 100 )^(1/4) - 1 = 9%
[Note - you can see how all the returns & portfolio growth formulas use the same multiplication as the geometric mean.]
Bad Mafs & Over Estimating Growth
If someone were to take the ‘average’ of the last 4 years of returns and tell you. And then if you used the ‘average’ return to project out your future expected portfolio growth, you would get very different numbers depending on which average you used.
Even in our simple example with only a 50bps difference in return results in a huge different ending value:

The easiest average to calculate is the arithmetic average. It is the one most people know. It is the one most people think of with average. And it is the one that gets used in these type of statements.
If you use a higher arithmetic average, it is easier to imply some low dollar amount will grow to over $1 million dollars over a long-enough time frame.
Remember, the arithmetic average will ALWAYS be larger than geometric average when looking at historical returns.
The graph above may look relatively close, but the ending values are ~$950,000 vs ~$1,130,000. You are getting almost 20% lower ending values from that 0.5% difference, nearly $200k.
Wrap-up: Arithmetic vs Geometric Mean
Using the arithmetic average when referencing prior returns should be a jailable offense, particularly if done in a way that over estimates the future portfolio growth.

Even using a 4-year history, you can see how quickly arithmetic and geometric averages can start to differ.
In the subscriber only post later this week, we will continue to build on our retirement projection knowledge. We will go over all the reasons that “Your Lifetime Average Returns” don’t actually mean what you think they mean. Using the incorrect average is just one small issue in the larger problem of overestimating future portfolio growth.
Remember, increasing your income & increasing your savings rate by avoiding massive lifestyle creep is still your best bet. You can splurge once you make.
Until next time, remember “Don’t Use The Wrong Mean Or You’ll be Off Central…While Drinking Your Juice In The Hood”