[Note - We are transitioning articles from our prior site to substack and posting as free posts. This post is one being transitioned. Enjoy the bonus.]
Quick Summary
The term ‘average’ is misused in articles – sometimes due to midwit writers and other times to mislead the reader
I define the difference in 3 mathematical measures for average vs. the common usage in language
I’ll show examples of why only knowing the average of a group is useless
You will know more than 90% of people after reading
Farts Travel 7 Miles Per Hour On Average.
Is that true?
No idea. But I’d bet that knowing the average speed of a fart is just as useful to your success as any other advice you get that uses the words “on average”.
Why?
Averages tend to me a poor measure to make any decision based on.
However, if you are like me, your first thought was “7 mph, I could easily blow that away” (Yes my internal monologue is exclusively dad-puns). Or maybe you began to feel insecure about your own sphincter prowess. Fear not.
By the end of the post, you will know enough about averages to question the fact. Let’s jump right in.
What Is Meant By “Average”?
Which form of the word average is being used?
There is a mathematical definition for average, but there is also common language usage of the term.
In common language, average means ‘typical’, ‘common’, or ‘not extraordinary’. For example, “that was an average meal”.
In math, average is a measure to represent the center of dataset. Mathematical average usually refers to one of the 3 main measures of central tendency, the most common being the ‘mean’, but also including the ‘median’ and the ‘mode’.
Lastly, there is the misuse of average. This is the logical fallacy where the writer means to say ‘expected outcome’ and instead says average. Think about flipping a coin and getting heads 5 times in a row. What is the next flip? If you said “the next flip a tails is due to happen” you are committing this false logic. Each flip has 50/50 chance and each flip has no memory of prior flips. A heads is just as likely to come up as a tails on flip 6. The flawed thinking is the Law of Averages – hence my clever title that the average (common use) reader likely didn’t laugh at.
For example, if I were to say, “the next batter up is an average hitter with a .250 batting average. He is 0 for 3 today, but averages 1 hit every 4 times at bat so he should get on base”. The first average is the common use of the word meaning he is a so-so or common batter. The batting average is a mathematical measure. The last average is using the logical fallacy of him being ‘due’ for a hit.
Baseball is boring. For the sake of the rest of the post we will deal with anal acoustics. Therefore, lets assume a team of scientist convinced some rich folk to pay for a grant so they could study the wind velocity of thousands of butt blasts. Then they compiled the data from all the heinie hiccups and calculated an average speed.
But wait, didn’t you say there are 3 mathematical averages…which did they use?
3 Mathematical Averages
When most people say average, they are referring to the mean. The mean of a data set is calculated by adding up all the numbers and dividing by the count of the numbers. You have a fair 6-sided die. You add up 1+2+3+4+5+6 and divide by 6 sides to get an average of 3.5 per roll.
The median is the number where half of the values are lower and half the values are higher. Back to the die. The median would also be 3.5, as you would have 3 outcomes lower {1,2,3} and 3 outcomes greater {4,5,6}.
The mode is the number that appears the most in the set of data. If the results are {1,2,2,2,98}, the mode is 2 as it appears three times and the other numbers only appear once.
Here is an example to help understand. In the data below you will see 10 people and their measured toot speed and the calculations of the averages of the data.
The 2 tables are the same data showed sorted and unsorted
To calculate the mean, you sum all the speeds and divide by the count of the 10 pieces:
Sum: 1+3+3+3+3+4+5+6+6+36=70
Mean = 70 / 10 = 7mph average speed
To find the median you can use the sorted data table. Since there are 10 data points, the median is the number between the 5th and 6th value. (Note if there is an odd number the median would be an actual data point)
The 5th largest value is 3 and the 6th largest value is 4
The median is 3.5
The mode is the number that appears the most times
The value 3 appears four times and therefore the mode is 3
Therefore, the mathematical average could be 7mph if you use the mean, or 3.5mph if you use the median, or even 3mph if you use the mode. All 3 could be considered the average of the set. However, the 7mph mean value is the most likely.
Why Average Is A Poor Measure
Now that you see how to calculate the averages, note a few other interesting takeaways from above:
The mean of the data is 7 mph, but no actual person shot a bottom cannon off at that actual speed
This goes back to the law of averages fallacy. If you were to guess that since the average tushy turbine was 7 mph, the most likely measurement was 7mph you would be wrong.
The mode tells you the most common measurement is 3.
9 of the 10 people were below the 7 mph mean and one person is the Louie Armstrong of fruitti tutti booty tooties
The mean is heavily influenced by outliers – a small number of results far from the the cluster where most results are
Both the median and mode are well below the mean value due to the outlier

Why do you care?
This is one of the issues with articles just quoting a single number with no other information. At the beginning of the article, 7mph probably seemed like what most people passed gas at.
Now you should see that the average may not actually tell you anything useful. Looking at the sample above, most people actually vent stinks at half the 7mph speed. Therefore, by quoting 7mph average, the writer would be factually correct, but misleading the reader on what the actual results are.
How Symmetry Impacts Averages
When you think of an average, you likely think of a bell curve. The curve is symmetric (aka you can fold it in half and it matches) and in this case, the average is a fairly good measure.
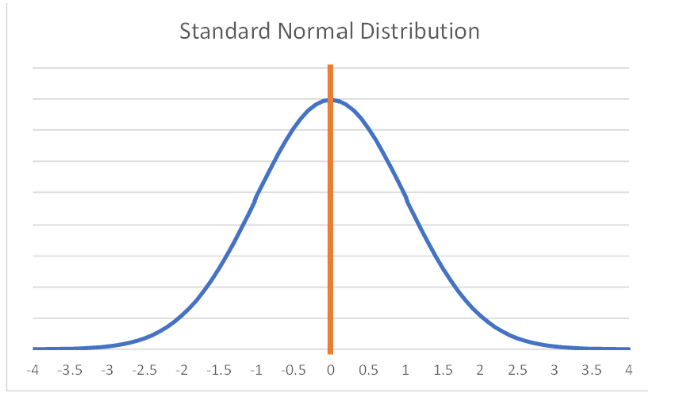
The mean, median, and mode are all the same and right at the peak of curve. It is marked by the orange line. This would be an instance that quoting just an average is ok. However, you can have 2 curves with different heights and different tails so you would also want some measure of dispersion.
A nice standard bell curve rarely happens in the real-world.
For one, negatives don’t always work in real-life. For instance, what is a negative fart?
Is it when you go with the chili for lunch and spend the afternoon with your office door closed making a personal gas chamber. But then after a particularly pungent stink burger, friggin Susan knocks on the door with a question. So you do what any self-respecting person does, and quickly try to inhale gulps of sulfur like a one-man air purifier. Is it science? Absolutely. Does it work? Susan’s teary eyes say no, but her boddd-y, her boddyyyy...actually that also says no, it doesn’t work. Next time you will think twice before asking about TPS report formatting Susan.

Point being, negative farts aren’t a thing.
However, vegans are a thing. And every vegan I know has this weird issue where they have this continual tail wind. Its like a balloon with a pinhole. Almost as if they are so full of smugness that the gas has no where to go but slowly leak out. This isn’t a 7mph fart. It is a 1mph hiss. What happens if we add some weak cheek vegans to our nice graph?.
The average of this chart is still 7mph. However, you see that most people have a strong tail propulsion of 8mph average, while the vegan bump at less than 1 mph is dragging everyone down.
This is common when you have a limit to a data set. Since negative farts aren’t a thing, you will tend to see a little cluster near 0.
To hop on my soapbox, there is a serious issue to address. Even to this day, my gram gram will walk down to her basement to old lady crop dust so that my grandfather doesn’t know. She is on metformin. A side affect of which is wicked gas. Poor grandma Esther is up and down those steps 1000 times a day due to the unfair expectations the patriarchal society she grew up in put on her. Granted, she can still crack a walnut with her thighs at 98 years old from all that stair climbing so not all bad. But lets assume that due to repressing women’s farts, there is an inequality between males and females with the force applied. Men have years of practice trying to make louder and more powerful rips. Let’s call it the “speed farts come inequality gap”. We can shorten this to just farts-come inequality. The result of this could lead to 2 distinct populations.
You can see that there is one population with an average speed of 3mph and another with a speed of 10mph. Even though the total average ends up being 7mph, nearly nobody has an actual 7mph duck call.
Wrapping Up – You Now Have An Above-Average Understanding Of Averages
Congrats! By reading this long post of fart jokes, you know more about how writers misuse and abuse the words ‘on average’ than 95% of the world.
Writers will:
Confuse a mathematical calculation and a common use of the term leading them to treat a calculated average as just another way to say ‘ordinary/general’
Not understand average can refer to ‘mean’, ‘median’, or ‘mode’
Not know averages are best when you have a similar population that forms a relatively symmetrical distribution, and are not a good measure when you have any of the following:
Outliers (aka Louie Armstrong powerful butt trumpet) – Data very far from the rest of the population that drags the overall average up/down
Limits (aka Vegans not able to get skunk bait at a negative speed) – If there is a natural threshold, there tends to be a lump of results near it. Typically this can be seen around 0 if you are dealing with something that can’t go negative
Dissimilar populations (aka farts-come inequality) – The average of 2 dissimilar populations doesn’t tell you much of either
Not provide any detail to ascertain how to interpret the average.
We don’t know if 7mph was calculated off 1 person over time, surprise farts or forced farts, age measured, meals before measuring, over or under the underwears, etc.
I had fun with the topic as it tends to be dry. But the takeaways are valid. If you are given a fact about an average, especially in an article trying to give advice or form your opinion, immediately question the number and start asking some of the above questions.
Is this mathematical or common language? Which measure? What is the distribution? Are there outliers? Is the underlying population consistent? How was the measuring done? etc.
The biggest abuse you see in personal finance is when someone refers to “an average millionaire” and says things like “the average millionaire drives an 8 yr old car”. A millionaire can be someone with $1,000,000.01 all the way to $999,999,999.99 in that bucket. A boomer who bumbled their way through the best equity market ever to save $1mm isn’t inspiring as the guy who bootstrapped his way to $100mm.
“There are 3 kinds of lies: Lies, Damned Lies, and Statistics”
-popularized by Mark Twain
The concept of averages not being a great source of information is nothing new.
If you really want to impress the ladies/fellas at your next event, find a way to drop a reference to Anscombe’s Quartet.
All 4 data sets have the same averages, as well as other simple statistics like line of best fit. Without graphing the data you would assume they were all very similar.
If an article was to give you the average, you wouldn’t know which of the 4 very different sets of orange dots it could be.
However by being vague, it allows bad actors to make any argument they want with the data. Hence why some form of the saying “lies, damned lies, and statistics” has hung around for a while.
One of my upcoming posts will hit on this concept with the college decision advice that routinely gets thrown around. Both average student loans and average increase in starting salary.








